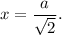Question

The electric field along the axis of a ring-shaped charge of total charge Q distributed uniformly is given by E = Qx/(4π o(x2 + a2)3/2) where a is the radius of the ring and x is the distance from the center of the ring. The electric field at the center of the ring is zero and at great distances from the ring approaches zero. At what position is the electric field a maximum for positive values of x?

Answer 1

The electric field intensity as a function of the distance
`x` from the center of the ring is given by:

`E(x) = (Qx)/(4\pi\varepsilon_0 (x^2 + a^2)^(3/2)).`

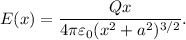
Taking the derivative of
`E` with respect to
`x`, we get:

`\frac{\textrm{d}E}{\textrm{d}x} = (Q)/(4\pi\varepsilon_0)\frac{\textrm{d}}{\textrm{d}x}\left[(x)/((x^2 + a^2)^(3/2))\right].`

We will now use the quotient rule:

`\frac{\textrm{d}}{\textrm{d}x}\left[(x)/((x^2 + a^2)^(3/2))\right] = \frac{\frac{\textrm{d}x}{\textrm{d}x}(x^2+a^2)^(3/2) - x\frac{\textrm{d}}{\textrm{d}x}\left[(x^2+a^2)^(3/2)\right]}{\left[(x^2+a^2)^(3/2)\right]^2}.`

We now use the chain and power rules to get:

`\frac{\textrm{d}}{\textrm{d}x}\left[(x^2+a^2)^(3/2)\right] = (3)/(2)(x^2+a^2)^(1/2)\frac{\textrm{d}}{\textrm{d}x}(x^2 + a^2) = (3)/(2)√(x^2 + a^2)2x = 3x√(x^2 + a^2).`

And also:

`\frac{\textrm{d}x}{\textrm{d}x} = 1.`

The derivative is then:

`\frac{\textrm{d}E}{\textrm{d}x} = (Q)/(4\pi\varepsilon_0)((x^2+a^2)^(3/2) - 3x^2√(x^2 + a^2))/((x^2+a^2)^3).`

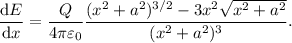
Since the denominator is never zero and
`Q \\eq 0`, we can write:

`\frac{\textrm{d}E}{\textrm{d}x} = 0 \iff(x^2+a^2)^(3/2) - 3x^2√(x^2 + a^2) = 0 \iff (x^2 + a^2)^(3/2) = 3x^2√(x^2+a^2).`

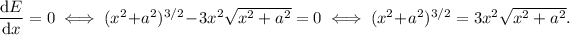
Dividing both sides of the equation by
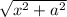`√(x^2+a^2)`, we get:

`x^2 + a^2 = 3x^2 \iff 2x^2 = a^2 \iff x^2 = (a^2)/(2) \iff x = \pm (a)/(√(2)), \textrm{ with } a > 0.`

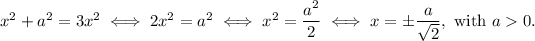
We now need to check whether this is a maximum, a minimum or a saddle point. We can use the second derivative test, but there's an easier way. Since
`E(0) = 0`,
`\lim\limits_(x \to \infty)E(x) = 0` and
`E(x) > 0` for
`x > 0`,
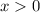`E` necessarily has a maximum, since
`E` is continuous.

Since we want positive values of
`x`, the solution is:

`x = (a)/(√(2)).`