The velocity of the car after 10 s is 78.95 km/hr
Step-by-step explanation:
Given:
m = 1,250 kg
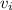 = 30 km/hr
= 30 km/hr
F = 1,700 N
t = 10 s
Required:
Final velocity
Equation:
Force
F = ma
where: F - force
m - mass
a - acceleration
Acceleration
a =
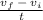
where: a - acceleration
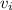 - initial velocity
- initial velocity
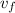 - final velocity
- final velocity
t - time elapsed
Solution:
Solve for acceleration using the formula for force
F = ma
Substitute the value of F and m
(1700 N) = (1250 kg)(a)
a =
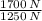
a = 1.36 m/s²
Solve for final velocity using the formula for acceleration
=
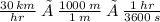
=
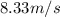
- Substitute the value of a,
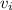 and t
and t
a =
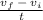
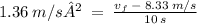
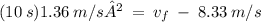
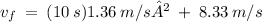
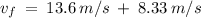
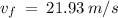
=

=

Final answer
The velocity of the car after 10 s is 78.95 km/hr