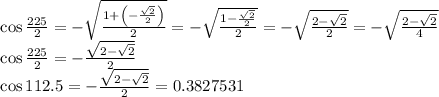Question

What is the exact value of cos112.5?

Answer 1

The answer is -0.382683432 if 112.5 is in degrees

Answer 2

The exact value of cos⁡ 112.5 is
`\bold{-\frac{\sqrt{(2-√(2))}}{2}= 0.3827531}`

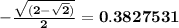
Solution:

Use half angle formula for Cos,

`\begin{array}{l}{\cos \left((x)/(2)\right)=\pm \sqrt{(1+\cos x)/(2)}} \\ {\cos 112.5=\cos (225)/(2)=-\sqrt{(1+\cos 225)/(2)} \quad(\text { equation } 1)}\end{array}`

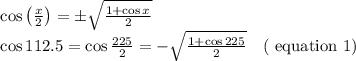
(Since cos 112.5 is in II quadrant ,negative sign is used)

cos⁡ 225 = cos⁡ (45+180)

cos ⁡(a+b) = cos a cos b+sin a sin⁡ b

cos ⁡(45+180) = cos 45 cos⁡ 180+ sin⁡ 45 sin ⁡180

`\begin{array}{l}{\cos 45=(√(2))/(2)} \\ \\ {\sin 45=(√(2))/(2)}\end{array}`

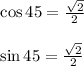
cos⁡ 180 = -1

sin⁡ 180 = 0

`\begin{array}{l}{\cos (45+180)=(√(2))/(2)(-1)+(√(2))/(2)(0)} \\\\ {\cos (45+180)=-(√(2))/(2)+0} \\\\ {\cos (45+180)=-(√(2))/(2)(\text { equation } 2)}\end{array}`

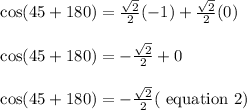
apply equation 2 in equation 1

`\begin{array}{l}{\cos (225)/(2)=-\sqrt{(1+\left(-(√(2))/(2)\right))/(2)}=-\sqrt{(1-(√(2))/(2))/(2)}=-\sqrt{(2-√(2))/(2)}=-\sqrt{(2-√(2))/(4)}} \\ {\cos (225)/(2)=-\frac{\sqrt{2-√(2)}}{2}} \\ {\cos 112.5=-\frac{\sqrt{2-√(2)}}{2}}=0.3827531\end{array}`