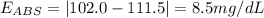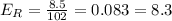Answer:
A. 96.3 mg/dL
Absolute error: 5.7 mg/dL
Relative error: 5.6%
B. 97.2 mg/dL
Absolute error: 4.8 mg/dL
Relative error: 4.7%
C. 104.8 mg/dL
Absolute error: 2.8 mg/dL
Relative error: 2.7%
D. 111.5 mg/dL
Absolute error: 9.5 mg/dL
Relative error: 9.3%
E. 110.5 mg/dL
Absolute error: 8.5 mg/dL
Relative error: 8.3%
Step-by-step explanation:
The formula for the absolute error is:
Absolute error = |Actual Value - Measured Value|
The formula for the relative error is:
Relative error = |Absolute error/Actual value|
In your exercise, we have that
Actual Value = 102.0 mg/dL
A. 96.3 mg/dL:
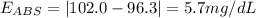
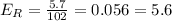
B. 97.2 mg/dL
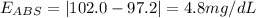
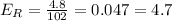
C. 104.8 mg/dL
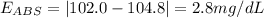
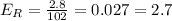
D. 111.5 mg/dL
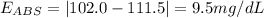
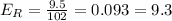
E. 110.5 mg/dL