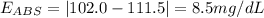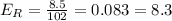Question

A blood sample with a known glucose concentration of 102.0 mg/dL is used to test a new at home glucose monitor. The device is used to measure the glucose concentration in the blood sample five times. The measured glucose concentrations are 96.3 , 97.2 , 104.8 , 111.5 , and 110.5 mg/dL. Calculate the absolute error and relative error for each measurement made by the glucose monitor. A. 96.3 mg/dL absolute error = mg/dL relative error = B. 97.2 mg/dL absolute error = mg/dL relative error = C. 104.8 mg/dL absolute error = mg/dL relative error = D. 111.5 mg/dL absolute error = mg/dL relative error = E. 110.5 mg/dL

Answer 1

A. 96.3 mg/dL

Absolute error: 5.7 mg/dL

Relative error: 5.6%

B. 97.2 mg/dL

Absolute error: 4.8 mg/dL

Relative error: 4.7%

C. 104.8 mg/dL

Absolute error: 2.8 mg/dL

Relative error: 2.7%

D. 111.5 mg/dL

Absolute error: 9.5 mg/dL

Relative error: 9.3%

E. 110.5 mg/dL

Absolute error: 8.5 mg/dL

Relative error: 8.3%

Step-by-step explanation:

The formula for the absolute error is:

Absolute error = |Actual Value - Measured Value|

The formula for the relative error is:

Relative error = |Absolute error/Actual value|

In your exercise, we have that

Actual Value = 102.0 mg/dL

A. 96.3 mg/dL:

`E_(ABS) = |102.0 - 96.3| = 5.7mg/dL`

`E_(R) = (5.7)/(102) = 0.056 = 5.6%`

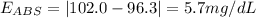
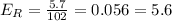
B. 97.2 mg/dL

`E_(ABS) = |102.0 - 97.2| = 4.8mg/dL`

`E_(R) = (4.8)/(102) = 0.047 = 4.7%`

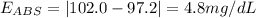
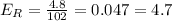
C. 104.8 mg/dL

`E_(ABS) = |102.0 - 104.8| = 2.8mg/dL`

`E_(R) = (2.8)/(102) = 0.027 = 2.7%`

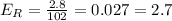
D. 111.5 mg/dL

`E_(ABS) = |102.0 - 111.5| = 9.5mg/dL`

`E_(R) = (9.5)/(102) = 0.093 = 9.3%`

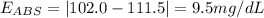
E. 110.5 mg/dL

`E_(ABS) = |102.0 - 111.5| = 8.5mg/dL`

`E_(R) = (8.5)/(102) = 0.083 = 8.3%`