Question

The dam cross section is an equilateral triangle, with a side length, L, of 50 m. Its width into the paper, b, is 100 m. The dam material has a specific gravity, SG, of 3.1. You may assume that the dam is loosely attached to the ground at its base, though there is significant friction to keep it from sliding.Is the weight of the dam sufficient to prevent it from tipping around its lower right corner?

Answer 1

Step-by-step explanation:

In an equilateral trinagle the center of mass is at 1/3 of the height and horizontally centered.

We can consider that the weigth applies a torque of T = W*b/2 on the right corner, being W the weight and b the base of the triangle.

The weigth depends on the size and specific gravity.

W = 1/2 * b * h * L * SG

Then

Teq = 1/2 * b * h * L * SG * b / 2

Teq = 1/4 * b^2 * h * L * SG

The water would apply a torque of elements of pressure integrated over the area and multiplied by the height at which they are apllied:

`T1 = \int\limits^h_0 {p(y) * sin(30) * L * (h-y)} \, dy`

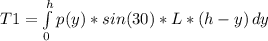
The term sin(30) is because of the slope of the wall

The pressure of water is:

p(y) = SGw * (h - y)

Then:

`T1 = \int\limits^h_0 {SGw * (h-y) * sin(30) * L * (h-y)} \, dy`

`T1 = \int\limits^h_0 {SGw * sin(30) * L * (h-y)^2} \, dy`

`T1 = SGw * sin(30) * L * \int\limits^h_0 {(h-y)^2} \, dy`

`T1 = SGw * sin(30) * L * \int\limits^h_0 {(h-y)^2} \, dy`

`T1 = SGw * sin(30) * L * \int\limits^h_0 {h^2 - 2*h*y + y^2} \, dy`

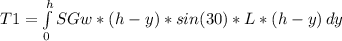
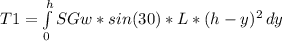
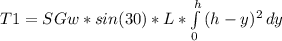
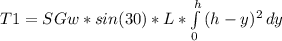
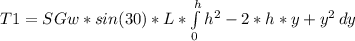
T1 = SGw * sin(30) * L * (h^2*y - h*y^2 + 1/3*y^3)(evaluated between 0 and h)

T1 = SGw * sin(30) * L * (h^2*h - h*h^2 + 1/3*h^3)

T1 = SGw * sin(30) * L * (h^3 - h^3 + 1/3*h^3)

T1 = 1/3 * SGw * sin(30) * L * h^3

To remain stable the equilibrant torque (Teq) must be of larger magnitude than the water pressure torque (T1)

1/4 * b^2 * h * L * SG > 1/3 * SGw * sin(30) * L * h^3

In an equilateral triangle h = b * cos(30)

1/4 * b^3 * cos(30) * L * SG > 1/3 * SGw * sin(30) * L * b^3 * (cos(30))^3

SG > SGw * 4/3* sin(30) * (cos(30))^2

SG > 1/2 * SGw

For the dam to hold, it should have a specific gravity of at leas half the specific gravity of water.

This is avergae specific gravity, including holes.