Question

Consider the flow of air through a wind turbine whose blades sweep an area of diameter D (in m). The average air velocity through the swept area is V (in m/s). On the bases of the units of the quantities involved, show that the mass flow rate (in kg/s) through the swept area is proportional to air density, the wind velocity, and the square of the diameter of the swept area.

Answer 1

Mass flow rate = ρ x A x V

Step-by-step explanation:

Given that

Diameter = D

Average velocity =V

We know that volume flow rate Q

Q = A x V

We know that mass,m

m= ρ x Volume

Mass flow rate = ρ x volume flow rate

Mass flow rate = ρ x A x V

Where

ρ is the density of air

V is the average velocity

A is the area of blades

We know that

`A=(\pi)/(4) D^2`

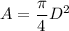
So from above equation we can say that

Mass flow rate is directly proportional to the density of air.

Mass flow rate is directly proportional to the average velocity of air.

Mass flow rate is directly proportional to the square of diameter of the swept area.