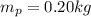Question

A 1.0-kg standard cart collides on a low-friction track with cart A. The standard cart has an initial x component of velocity of +0.40 m/s, and cart A is initially at rest. After the collision the x component of velocity of the standard cart is +0.20 m/s and the x component of velocity of cart A is +0.70 m/s . After the collision, cart A continues to the end of the track and rebounds with its speed unchanged. Before the carts collide again, you drop a lump of putty onto cart A, where it sticks. After the second collision, the x component of velocity of the standard cart is -0.20 m/s and the x component of velocity of cart A is +0.40 m/s .What is the inertia of the putty?

Answer 1

Step-by-step explanation:

Mathematically, linear momentum is expressed as the product of mass and velocity. Linear momentum conservation law states that a body or system of bodies retains its total momentum unless an external force is applied to the system.

In this case, the system consists of two carts.

At the start, the linear momentum (P) of the system is equal to:

`P=1.0kg*0.4m/s=0.4kg*m/s`

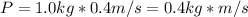
It's only composed of linear momentum of the standard cart because cart A doesn't have any linear momentum at that moment.

After the collision, linear momentum has to be the same

`P=0.4kg*m/s=1.0kg*0.20m/s+m_(A) *0.70m/s`

where m_A is the mass of the cart A.

Solving for m_A

`m_(A) =0.28kg`

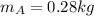
After the cart A rebounds, the linea momentum of the system has changed (because of the force present in the rebound). The new linear momentum is:

`P=1kg*0.2m/s+0.29kg*(-0.7m/s)=-0.003kg*m/s`

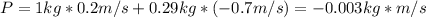
Then, the lump of putty is added to the system, but the linear momentum has to be the same, because we added a mass, not a force. The mass of that putty (m_p) has to be added to the equation of the system

`-0.003kg*m/s=1.0kg*(-0.2m/s)+(0.29kg+m_(p) )(0.4m/s)`

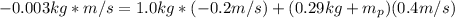
Solving for m_p

`m_(p)=0.20kg`