Question

Archaeologists can determine the age of artifacts made of wood or bone by measuring the amount of the radioactive isotope 14C present in the object. The amount of isotope decreases in a first-order process. If 18.7% of the original amount of 14C is present in a wooden tool at the time of analysis, what is the age of the tool? The half-life of 14C is 5,730 yr. Give your answer in scientific notation.

Answer 1

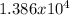`1.386x10^4` years.

Step-by-step explanation:

The half-life is the time needed to reduce in 50% the mass of the sample. So, imagine compound A, after its first half-life, it will have 0.5A. After its second half-life, will have 50% of the 0.5A! So, the mass will be 0.25A. So, the percentage of A, is given by:

`A = (0.5)^n`

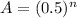
Where n is the quantitative of half-life. So, for 18.7% of C, or 0.187:

`0.187 = (0.5)^n`

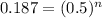
Applying log in both side of the equation:

`log(0.187) = log(0.5)^n`

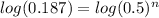
nlog(0.5) = log(0.187)

-0.301n = -0.728

n = 2.419 half-life

If one half-life is 5,730 yr, than 2.419 will be:

2.419x5730 = 13,860.870 yr

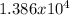`1.386x10^4` years.