Answer:
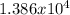 years.
years.
Step-by-step explanation:
The half-life is the time needed to reduce in 50% the mass of the sample. So, imagine compound A, after its first half-life, it will have 0.5A. After its second half-life, will have 50% of the 0.5A! So, the mass will be 0.25A. So, the percentage of A, is given by:
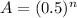
Where n is the quantitative of half-life. So, for 18.7% of C, or 0.187:

Applying log in both side of the equation:

nlog(0.5) = log(0.187)
-0.301n = -0.728
n = 2.419 half-life
If one half-life is 5,730 yr, than 2.419 will be:
2.419x5730 = 13,860.870 yr
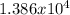 years.
years.