Answer:
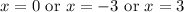
Explanation:
We have been an equation
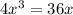 . We are asked to find the solutions for our given equation.
. We are asked to find the solutions for our given equation.
First of all, we will subtract
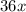 from both sides as:
from both sides as:
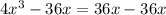
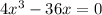
Let us factor the given equation.
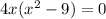
Use difference of squares:
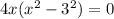
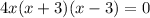
Using zero product property, we will get:
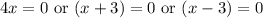
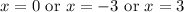
Therefore, the solutions for our given equation would be
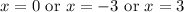 .
.