Answer:
Mean =43,935.9
Median = 41,433
Explanation:
We are given the following data:
Number of observations = 10
38364, 39143, 39619, 40742, 41038, 41828, 45289, 48960, 49863, 54513
Formula:
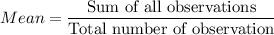
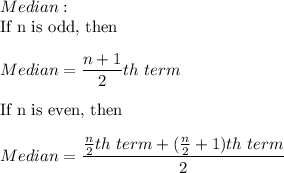
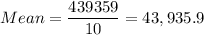
Sorted data:
38364, 39143, 39619, 40742, 41038, 41828, 45289, 48960, 49863, 54513

Median is the value that divides the data into two equal halves. Hence, median best describes the center of the data set.