Question

Monochromatic light with wavelength 690 nm is incident on a slit with width 0.0329 mm. The distance from the slit to a screen is 3.2 m. Consider a point on the screen 1.3 cm from the central maximum. Calculate (a) θ for that point, (b) α, and (c) the ratio of the intensity at that point to the intensity at the central maximum.

Answer 1

Explanation:

We have given,

`Wavelength\ of the\ light(\lambda)} = 690mm = 690 * 10^(-9)m`

`\text {width of the slit(w)} = 0.0329\ mm = 0.0329 * 10^(-3)m`

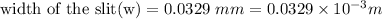
distance of the slit from the screen(d) = 3.2m

distance from the central maximum(m) = 1.3cm = 0.013m

Now,

(a). The expression for the angle of the inclination of the wave is (
`\theta` )

`\theta = sin^(-1) \frac md\\\theta = sin^(-1)( \frac {0.013}{3.2})\\\\\theta = sin^(-1)(0.0040625)\\\\\theta = sin^(-1)(sin 0.23^o)`

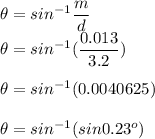
Thus the angle of inclination of the wave is

`\theta= 0.23^o`

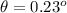
(b). The expression for the angle
`\alpha`

`\alpha = \frac {\pi * w}{\lambda} sin \theta\\\alpha = \frac {3.14 * 0.0329 * 10^(-3)}{690 * 10^(-9)} sin {0.23^o}\\\\\alpha = \frac {3.14 * 0.0329 * 10^(-3) * 0.004.625}{690 * 10^(-9)}`

after solving the equation we get,

Thus the angle
`\alpha` = 0.61 radian

(c). the expression for the ratio of the intensity is

`(I_0)/(I) = (\frac {sin \alpha}{\alpha}) ^2`

`(I_0)/(I) = (\frac {sin (0.61)}{0.61})^2\\(I_0)/(I) = (\frac {0.0.65}{0.61})^2\\(I_0)/(I) = 0.0305`

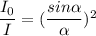
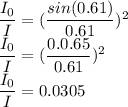
Thus the ratio of the intensity is 0.0305