Answer:

Explanation:
Let an equation of the plane
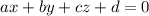
We have to find the equation of the plane consisting of all points that are equidistant from (-3,5,-4) and (-5,0,4).
The coefficient of x=-2
Distance formula=
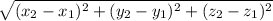
Let
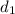 be the distance of point (x,y,z)lie on the plane and point (-3,5,-4).
be the distance of point (x,y,z)lie on the plane and point (-3,5,-4).
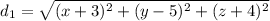
Let
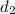 be the distance between the point (x,y,z) lie on the plane and the point (-5,0,4).
be the distance between the point (x,y,z) lie on the plane and the point (-5,0,4).

According to question
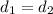
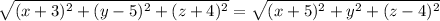
Squaring on both sides
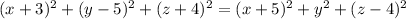
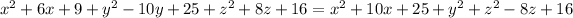
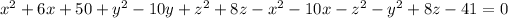
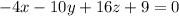
Divided the equation by 2
