Question

A bag of sand originally weighing 144 lb was lifted at a constant rate. As it rose, sand also leaked out at a constant rate. The sand was half gone by the time the bag had been lifted to 10 ft. How much work was done lifting the sand this far? (Neglect the weight of the bag and lifting equipment.)

Answer 1

The work done was W=720lb.ft

Step-by-step explanation:

Here weight is a lineal function of the vertical position. Let's put it in the following way:

`w(y)=ay+b`

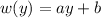
where w is the weight and y is the vertical position (how high it is the bag).

So, from the information given:

`w(0)=144lb` ⇒
`a0+b=b=144lb`

`w(10ft)=(144lb)/(2) =72lb` ⇒
`a10ft+b=a10ft+144lb=72lb` ⇒
`a=(72lb-144lb)/(10ft) =-7.2(lb)/(ft)`

∴
`w(y)=-7.2(lb)/(ft)y+144lb`

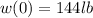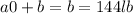
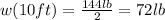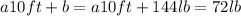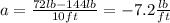
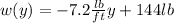
So, the work done will be:

`W=\int\limits^(10ft)_0 {w(y)} \, dy =\int\limits^(10ft)_0 {-7.2(lb)/(ft)y+144lb} \, dy = \int\limits^(10ft)_0 {-7.2(lb)/(ft)y} \, dy + \int\limits^(10ft)_0 {144lb} \, dy=`

`= -7.2(lb)/(ft)(1)/(2) ((10ft)^2-0^2) + 144lb. 10ft=720lb.ft`

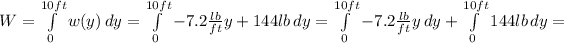
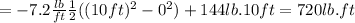
∴ W=720lb.ft