Answer:
The work done was W=720lb.ft
Step-by-step explanation:
Here weight is a lineal function of the vertical position. Let's put it in the following way:
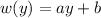
where w is the weight and y is the vertical position (how high it is the bag).
So, from the information given:
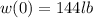 ⇒
⇒
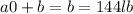
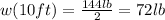 ⇒
⇒
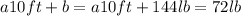 ⇒
⇒
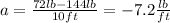
∴
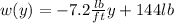
So, the work done will be:
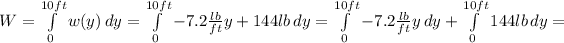
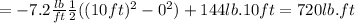
∴ W=720lb.ft