Question

A small first-aid kit is dropped by a rock climber who is descending steadily at 1.9 m/s. After 2.4 s, what is the velocity of the first-aid kit? The acceleration of gravity is 9.81 m/s 2 . Answer in units of m/s.

Answer 1

`v_f=25.444\ m/s`

Step-by-step explanation:

All given this are:

Initial velocity is ,
`v_i=1.9\ m/s`

Time taken,
`t=2.4 \ s`

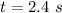
The acceleration due to gravity is ,
`g=9.81 \ m/s^2`

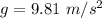
So , we need to find final velocity,
`v_f`.

So we will use equation of motion.

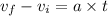`v_f-v_i=a* t`. Here a is acceleration which is g .

putting all those values.

`v_f=1.9 + 9.81*2.4=25.444\ m/s`.

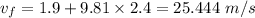Hence , it is the required solution.

Answer 2

`v=-21.65 m/s`

Step-by-step explanation:

From the exercise we have:

`v_(o)=1.9m/s\\ g=9.81 m/s^(2)\\ t=2.4s`

To find the velocity after 2.4s we need to use the following formula:

`v=v_(o)+gt`

`v=1.9m/s-(9.81m/s^(2))(2.4s)=-21.65m/s`

The negative sign means that the kit is going down.