Question

Maxwell scored 890 on the SAT. The distribution of SAT scores in a reference population is

normally distributed with mean 1100 and standard deviation 140. Jonah scored 21 on the ACT. The
distribution of ACT scores in a reference population is normally distributed with mean 22 and
standard deviation 3. Who performed better on the standardized exams and why?

Maxwell scored higher than Jonah. Maxwell's score was an 890, which is greater than
Jonah's score of 21.

Maxwell scored higher than Jonah. Maxwell's standardized score was -1.5, which is 1.5
standard deviations below the mean but further from the mean than Jonah's standardized
score of -0.33 standard deviations below the mean.

Jonah scored higher than Maxwell. Maxwell's score was 210 points below the mean of
1100 and Jonah's was 1 point below the mean of 22

Jonah scored higher than Maxwell. Jonah is only 15 points from the top score of 36 on
the ACT and Maxwell is 710 points from the top score of 1600 on the SAT.

Jonah scored higher than Maxwell. Jonah's standardized score was -0.33, which is 0.33
standard deviation below the mean and Maxwell's standardized score was -1.5, which is
1.5 standard deviations below the mean.

Answer 1

Last Option

Explanation:

Since, the scores of two different tests are mentioned, we cannot compare the scores as it is. In order to compare the scores they should be in similar form. One way to do this is to convert the scores into their equivalent z scores and then do the comparison. A higher z score will indicate a better performance.

Scores of Maxwell:

Scores of maxwell = x = 890

Mean scores of the distribution in SAT exams = u = 1100

Standard deviation of scores =
`\sigma` = 140

The formula for the z scores is:

`z=(x-u)/(\sigma)`

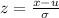
Using the values in this formula, we get:

`z=(890-1100)/(140)=-1.5`

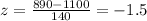
Scores of Jonah:

Scores of Jonah = x = 21

Mean scores of distribution of ACT exams = u = 22

Standard deviation =
`\sigma` = 3

Using the values in the formula, we get the z score as:

`z=(21-22)/(3)=-0.33`

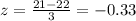
Conclusion:

Thus, the z score of Maxwell is -1.5, which indicates that the scores of Maxwell were 1.5 standard deviations below the mean. The z score of Jonah is -0.33, which indicates that the scores of Jonah were 0.33 standard deviations below the mean.

Since the scores of Maxwell is more lower, or the scores of Jonah are higher, we can conclude that Jonah scores higher than Maxwell.

Hence, the correct option is:

Jonah scored higher than Maxwell. Jonah's standardized score was -0.33, which is 0.33 standard deviation below the mean and Maxwell's standardized score was -1.5, which is 1.5 standard deviations below the mean.