Answer:
Last Option
Explanation:
Since, the scores of two different tests are mentioned, we cannot compare the scores as it is. In order to compare the scores they should be in similar form. One way to do this is to convert the scores into their equivalent z scores and then do the comparison. A higher z score will indicate a better performance.
Scores of Maxwell:
Scores of maxwell = x = 890
Mean scores of the distribution in SAT exams = u = 1100
Standard deviation of scores =
 = 140
= 140
The formula for the z scores is:
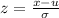
Using the values in this formula, we get:
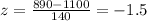
Scores of Jonah:
Scores of Jonah = x = 21
Mean scores of distribution of ACT exams = u = 22
Standard deviation =
 = 3
= 3
Using the values in the formula, we get the z score as:
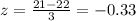
Conclusion:
Thus, the z score of Maxwell is -1.5, which indicates that the scores of Maxwell were 1.5 standard deviations below the mean. The z score of Jonah is -0.33, which indicates that the scores of Jonah were 0.33 standard deviations below the mean.
Since the scores of Maxwell is more lower, or the scores of Jonah are higher, we can conclude that Jonah scores higher than Maxwell.
Hence, the correct option is:
Jonah scored higher than Maxwell. Jonah's standardized score was -0.33, which is 0.33 standard deviation below the mean and Maxwell's standardized score was -1.5, which is 1.5 standard deviations below the mean.