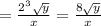Answer: Last option.
Explanation:
Given the expression:
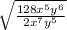
The Quotient of powers property states that:
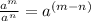
And the Power of a powet property states that:
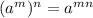
Then, applying these properties, you get:
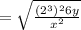
Now you must remember that:
![\sqrt[a]{a^n}=a](https://img.qammunity.org/2020/formulas/mathematics/middle-school/3eo2xi7ssgi7hcej46squkcw9m19ckaqpi.png)
Therefore, simpliying the expression, you get: