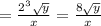Question

Which expression is equivalent to 128x^5y^6 \ 2x^7y^5 ? Assume x > 0 and y > 0.

Answer 1

D. 8√y/x

Explanation:

Answer 2

Answer: Last option.

Explanation:

Given the expression:

`\sqrt{(128x^5y^6)/(2x^7y^5)`

The Quotient of powers property states that:

`(a^m)/(a^n)=a^((m-n))`

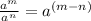
And the Power of a powet property states that:

`(a^m)^n=a^(mn)`

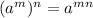
Then, applying these properties, you get:

`=\sqrt{((2^3)^26y)/(x^2)`

Now you must remember that:

`\sqrt[a]{a^n}=a`

Therefore, simpliying the expression, you get:

`=(2^3√(y))/(x)=(8√(y))/(x)`