Answer:
There is no solution for this system
Explanation:
I am going to solve this system by the Gauss-Jordan elimination method.
The Gauss-Jordan elimination method is done by transforming the system's augmented matrix into reduced row-echelon form by means of row operations.
We have the following system:
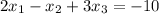
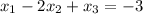
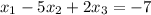
This system has the following augmented matrix:
![\left[\begin{array}{ccc}1&-3&4|-4\\3&-7&7|-8\\-4&6&-1|7\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/9zqkju8ns8ydmtlnvd67amtxi3c5jnb9st.png)
We start reducing the first row. So:
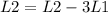
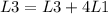
Now the matrix is:
![\left[\begin{array}{ccc}1&-3&4|-4\\0&2&-5|4\\0&-6&15|-9\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/x2jvikea8gqidaj1ytmyh9dg0kdbvtp3he.png)
We divide the second line by 2:
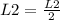
And we have the following matrix:
![\left[\begin{array}{ccc}1&-3&4|-4\\0&1&(-5)/(2)|2\\0&-6&15|-9\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/wnirxvpx56ki57l43tcc7ckhjgew2ybcm9.png)
Now we do:
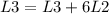
So we have
![\left[\begin{array}{ccc}1&-3&4|-4\\0&1&(-5)/(2)|2\\0&0&0|3\end{array}\right]](https://img.qammunity.org/2020/formulas/mathematics/college/n80vhbehdsa30nbinbicl463ok6hr3cbdc.png)
This reduced matrix means that we have:
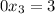
Which is not possible
There is no solution for this system