Question

Solve. X1 – 3x2 + 4x3 = -4 3xı – 7x2 + 7x3 = -8 –4x1 + 6x2 – x3 = 7

Answer 1

There is no solution for this system

Explanation:

I am going to solve this system by the Gauss-Jordan elimination method.

The Gauss-Jordan elimination method is done by transforming the system's augmented matrix into reduced row-echelon form by means of row operations.

We have the following system:

`2x_(1) - x_(2) + 3x_(3) = -10`

`x_(1) - 2x_(2) + x_(3) = -3`

`x_(1) - 5x_(2) + 2x_(3) = -7`

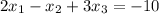
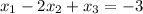
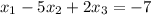
This system has the following augmented matrix:

`\left[\begin{array}{ccc}1&-3&4|-4\\3&-7&7|-8\\-4&6&-1|7\end{array}\right]`

We start reducing the first row. So:

`L2 = L2 - 3L1`

`L3 = L3 + 4L1`

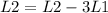
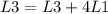
Now the matrix is:

`\left[\begin{array}{ccc}1&-3&4|-4\\0&2&-5|4\\0&-6&15|-9\end{array}\right]`

We divide the second line by 2:

`L2 = (L2)/(2)`

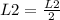
And we have the following matrix:

`\left[\begin{array}{ccc}1&-3&4|-4\\0&1&(-5)/(2)|2\\0&-6&15|-9\end{array}\right]`

Now we do:

`L3 = L3 + 6L2`

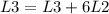
So we have

`\left[\begin{array}{ccc}1&-3&4|-4\\0&1&(-5)/(2)|2\\0&0&0|3\end{array}\right]`

This reduced matrix means that we have:

`0x_(3) = 3`

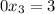
Which is not possible

There is no solution for this system