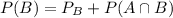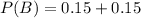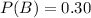1 Answer

Jtahlborn · Answer 1 · 2020-08-18T19:06:22+0000

Answer:

P(B) = 0.30

Explanation:

This is a probability problem that can be modeled by a diagram of Venn.

We have the following probabilities:

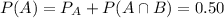
$P(A) = P_(A) + P(A \cap B) = 0.50$

In which
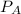P_(A) is the probability that only A happens.

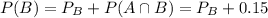
$P(B) = P_(B) + P(A \cap B) = P_(B) + 0.15$

To find P(B), first we have to find
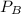P_(B) , that is the probability that only B happens.

Finding
P_(B) :

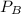The problem states that P(A OR B) = 0.65. This is the probability that at least one of this events happening. Mathematically, it means that:

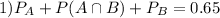
$1) P_(A) + P(A \cap B) + P_(B) = 0.65$

The problem states that P(A) = 0.5 and
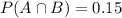$P(A \cap B) = 0.15$ . So we can find
P_(A) .

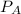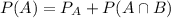
$P(A) = P_(A) + P(A \cap B)$

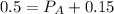
0.5 = P_(A) + 0.15

P_(A) = 0.35

Replacing it in equation 1)

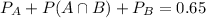
$P_(A) + P(A \cap B) + P_(B) = 0.65$

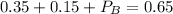
0.35 + 0.15 + P_(B) = 0.65

P_(B) = 0.65 - 0.35 - 0.15

P_(B) = 0.15

Since

$P(B) = P_(B) + P(A \cap B)$

P(B) = 0.15 + 0.15

P(B) = 0.30

Please log in or register to add a comment.