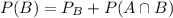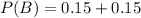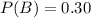Answer:
P(B) = 0.30
Explanation:
This is a probability problem that can be modeled by a diagram of Venn.
We have the following probabilities:
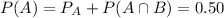
In which
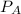 is the probability that only A happens.
is the probability that only A happens.
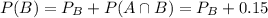
To find P(B), first we have to find
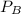 , that is the probability that only B happens.
, that is the probability that only B happens.
Finding
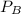 :
:
The problem states that P(A OR B) = 0.65. This is the probability that at least one of this events happening. Mathematically, it means that:
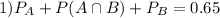
The problem states that P(A) = 0.5 and
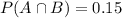 . So we can find
. So we can find
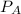 .
.
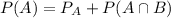
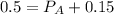

Replacing it in equation 1)
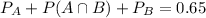
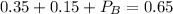


Since