Answer:
Change in momentum is
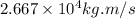
Solution:
The momentum of any body is the product of its mass and the velocity associated with the body and is generally given by:
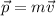
Now, as per the question:
Mass of the car, M = 1500 kg
The velocity in the east direction,

The velocity in the north direction,
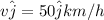
Now, the momentum of the car in the east direction:
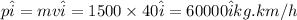
Now, the momentum of the car in the north direction:
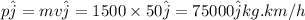
Change in momentum is given by:
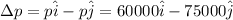
Now,
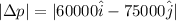
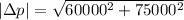
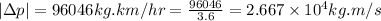
(Since,
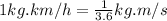 )
)