Answer:
Ans. the amount of time needed for the sinking fund to reach $25,000 if invested $255/month at 5.8% compounded monthly (Effective monthly=0.4833%) is 80.45 months.
Explanation:
Hi, first we need to transform that 5.8% compounded monthly into an effective monthly rate, that is as follows.

That means that our effective monthly rate is 0.483%
Now, we need to solve for "n" the following formula.
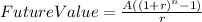
Let´s start solving
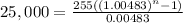
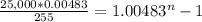

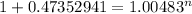
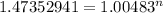
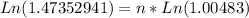
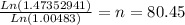
This means that it will take 80.45 months to reach $25,000 with an annuity of $255 at a rate of 5.8% compounded monthly (0.4833% effective monthly).
Best of luck.