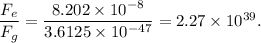Answer:
(a):
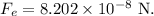
(b):
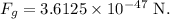
(c):
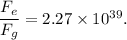
Step-by-step explanation:
Given that an electron revolves around the hydrogen atom in a circular orbit of radius r = 0.053 nm = 0.053
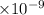 m.
m.
Part (a):
According to Coulomb's law, the magnitude of the electrostatic force of interaction between two charged particles of charges
 and
and
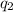 respectively is given by
respectively is given by
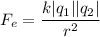
where,
 = Coulomb's constant =
= Coulomb's constant =
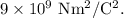
 = distance of separation between the charges.
= distance of separation between the charges.
For the given system,
The Hydrogen atom consists of a single proton, therefore, the charge on the Hydrogen atom,
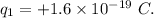
The charge on the electron,
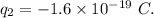
These two are separated by the distance,
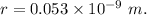
Thus, the magnitude of the electrostatic force of attraction between the electron and the proton is given by
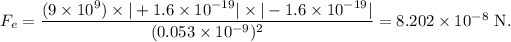
Part (b):
The gravitational force of attraction between two objects of masses
 and
and
 respectively is given by
respectively is given by
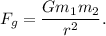
where,
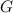 = Universal Gravitational constant =
= Universal Gravitational constant =

 = distance of separation between the masses.
= distance of separation between the masses.
For the given system,
The mass of proton,
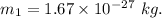
The mass of the electron,
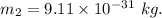
Distance between the two,
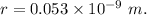
Thus, the magnitude of the gravitational force of attraction between the electron and the proton is given by
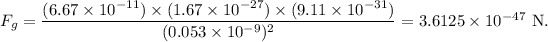
The ratio
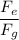 :
: