Answer:
The ball never passes 2m high, Hmax=1.27m
Step-by-step explanation:
we assume the ball doesn't bounce when it hits the ground.
We calculate the maximum height, Vf = 0.
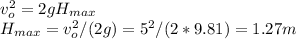
So, the ball never passes 2m high.
Kinematics equations:

Find annexed the graphics of x(t) and v(t)