Question

In the following pair of polynomials, the second polynomial is a factor of the first. Factor completely x^3+3x^2-18x , x-4

Answer 1

The required factors are: x, (x + 6) and (x - 3).

Explanation:

As per the question,

The given polynomial is:

`x^(3)+3x^(2)-18x`

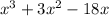
Now,

BY factorization, we get

`x^(3)+3x^(2)-18x`

`=x(x^(2)+3x-18)`

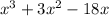
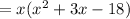
By splitting the mid-term, that is split 3x like:

3x = 6x - 3x

Therefore,

`x(x^(2)+6x-3x-18)`

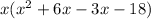
Now on further solving by taking common factor out, we get

`=x[x(x+6)-3(x+6)]`

`=x(x+6)(x-3)`

Therefore, the given second polynomial (x - 4), is not a factor of given polynomial
`x^(3)+3x^(2)-18x`.

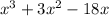Hence, the given polynomial has three factor x, (x + 6) and (x - 3).