Question

Find the expansion of tan x about the point X = 0.

Answer 1

`f(x) = x +(1)/(3)x^(3)+....`

Explanation:

As per the question,

let us consider f(x) = tan(x).

We know that The Maclaurin series is given by:

`f(x) = f(0) + (f^(')(0))/(1!)\cdot x+ (f^('')(0))/(2!)\cdot x^(2)+(f^(''')(0))/(3!)\cdot x^(3)+......`

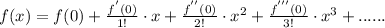
So, differentiate the given function 3 times in order to find f'(x), f''(x) and f'''(x).

Therefore,

f'(x) = sec²x

f''(x) = 2 × sec(x) × sec(x)tan(x)

= 2 × sec²(x) × tan(x)

f'''(x) = 2 × 2 sec²(x) tan(x) tan(x) + 2 sec²(x) × sec²(x)

= 4sec²(x) tan²(x) + 2sec⁴(x)

= 6 sec⁴x - 4 sec² x

We then substitute x with 0, and find the values

f(0) = tan 0 = 0

f'(0) = sec²0 = 1

f''(0) = 2 × sec²(0) × tan(0) = 0

f'''(0) = 6 sec⁴0- 4 sec² 0 = 2

By putting all the values in the Maclaurin series, we get

`f(x) = f(0) + (f^(')(0))/(1!)\cdot x+ (f^('')(0))/(2!)\cdot x^(2)+(f^(''')(0))/(3!)\cdot x^(3)+......`

`f(x) = 0 + (1)/(1)\cdot x+ (0)/(2)\cdot x^(2)+(2)/(6)\cdot x^(3)+......`

`f(x) = x +(1)/(3)x^(3)+....`

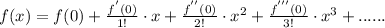
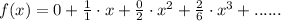
Therefore, the expansion of tan x at x = 0 is

`f(x) = x +(1)/(3)x^(3)+....`.