Question

Suppose the electrons and protons in 1g of hydrogen could be separated and placed on the earth and the moon, respectively. Compare the electrostatic attraction with the gravitational force between the earth and the moon. ( the number of atoms in 1g of hydrogen is Avogadro's number Na. There is one electron and one proton in a hydrogen atom. ) Please explain step by step

Answer 1

The gravitational force is 3.509*10^17 times larger than the electrostatic force.

Step-by-step explanation:

The Newton's law of universal gravitation and Coulombs law are:

`F_(N)=G m_(1)m_(2)/r^(2)\\F_(C)=k q_(1)q_(2)/r^(2)`

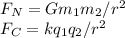
Where:

G= 6.674×10^−11 N · (m/kg)2

k = 8.987×10^9 N·m2/C2

We can obtain the ratio of these forces dividing them:

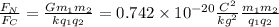`(F_(N))/(F_(C))=(Gm_(1)m_(2))/(kq_(1)q_(2))=0.742*10^(-20)(C^(2))/(kg^(2))(m_(1)m_(2))/(q_(1)q_(2))` --- (1)

The mass of the moon is 7.347 × 10^22 kilograms

The mass of the earth is 5.972 × 10^24 kg

And q1=q2=Na*e=(6.022*10^23)*(1.6*10^-19)C=9.635*10^4 C

Replacing these values in eq1:

`(F_(N))/(F_(C))}}=0.742*10^(-20)(C^(2))/(kg^(2))(7.347*5.972*10^(46)kg^(2))/((9.635*10^(4))^(2))`

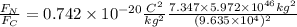
Therefore

`(F_(N))/(F_(C))}}=3.509*10^(17)`

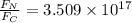
This means that the gravitational force is 3.509*10^17 times larger than the electrostatic force, when comparing the earth-moon gravitational field vs 1mol electrons - 1mol protons electrostatic field