Answer:
The gravitational force is 3.509*10^17 times larger than the electrostatic force.
Step-by-step explanation:
The Newton's law of universal gravitation and Coulombs law are:
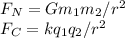
Where:
G= 6.674×10^−11 N · (m/kg)2
k = 8.987×10^9 N·m2/C2
We can obtain the ratio of these forces dividing them:
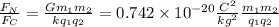 --- (1)
--- (1)
The mass of the moon is 7.347 × 10^22 kilograms
The mass of the earth is 5.972 × 10^24 kg
And q1=q2=Na*e=(6.022*10^23)*(1.6*10^-19)C=9.635*10^4 C
Replacing these values in eq1:
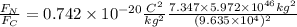
Therefore
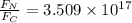
This means that the gravitational force is 3.509*10^17 times larger than the electrostatic force, when comparing the earth-moon gravitational field vs 1mol electrons - 1mol protons electrostatic field