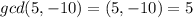Answer:
The greatest common divisor of two integers a and b (not both 0) is the largest integer that divides both a and b.
Explanation:
Think for example of the numbers a=5, and b= -10. The greatest common divisor of 5 and -10, is the largest integer that divides both 5 and -10. We can find it by inspection (although there are more advanced methods to find it). We can list all integers that divide both 5 and -10.
-5 divides 5, and it also divides -10
-1 divides 5, and it also divides -10
1 divides 5, and it also divides -10
5 divides 5, and it also dividies -10
The LARGEST of them all is then 5, so 5 is the greatest common divisor of 5 and -10. The usual way to write it is