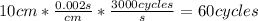Question

The time base on the oscilloscope is set for 2 ms/cm and the vertical input has a frequency of 3000 Hz. How many wave cycles will appear within the 10 cm width of the screen?

Answer 1

60 wave cycles

Step-by-step explanation:

As the horizontal axis in a oscilloscope represents time, the time base is simply the scale, in other words, the amount of time that each division of oscilloscope represents. Therefore, multiplying the width of the screen times the time base will give us the total amount of time graphed on the screen.

The frequency is the amount of oscillations or waves cycles per second. So, in order to find the total amount of oscillations:

`10cm *  (0.002 s)/(cm) *(3000cycles)/(s) = 60 cycles`

Answer 2

60 cycles

Step-by-step explanation:

The first thing we must do to solve the problem is to find how many cycles are presented in 1cm by multiplying the frequency by the base time of the

K=time base=2ms/cm=2x10-3s/cm

f=frecuency=3000s^-1

N=fk

N=(3000)(2x10^-3)=6cycles/cm

Ntot=6x10=60cycles