Question

Are the points (-4,-1), (2,1) and (11,4) collinear? Justify your answer.

Answer 1

Answer: Yes , the points (-4,-1), (2,1) and (11,4) are collinear.

Explanation:

We know that if three points
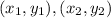`(x_1,y_1),(x_2,y_2)` and
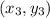`(x_3,y_3)` are collinear, then their area must be zero.

The area of triangle passes through points
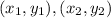`(x_1,y_1),(x_2,y_2)` and
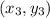`(x_3,y_3)` is given by :-

`\text{Area}=(1)/(2)|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|`

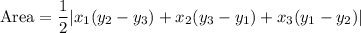
Given points : (-4,-1), (2,1) and (11,4)

Then, the area of ΔABC will be :-

`\text{Area}=(1)/(2)|-4(1-4)+(2)(4-(-1))+(11)(-1-1)|\\\\\Rightarrow\text{Area}=(1)/(2)|-4(-3)+(2)(5)+(11)(-2)||\\\\\Rightarrow\text{Area}=(1)/(2)|12+10-22|\\\\\Rightarrow\text{Area}=(1)/(2)|0|=0`

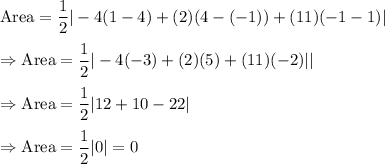
Hence, the points (-4,-1), (2,1) and (11,4) are collinear.