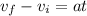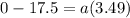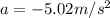Answer:
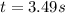
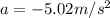
Step-by-step explanation:
As we know that initial speed of the cheetah is given as
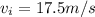
finally it comes to rest so final speed is given as
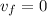
now we know that distance covered by cheetah while it stop is given as
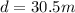
now by equation of kinematics we know that
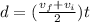
here we have
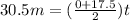
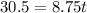
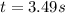
Now in order to find the acceleration we know that