Question

Suppose you made 5 measurements of the speed of a rocket:10.2 m/s, 11.0 m/s, 10.7 m/s, 11.0 m/s and 10.5 m/s. From these measurements you conclude the rocket is traveling at a constant speed. Calculate the mean, standard deviation, and error on the mean.

Answer 1

Mean = = 10.68 m/s

Standard deviation = σ = 0.342 m/s

Error = 0.153 .

Step-by-step explanation:

The data has 5 readings.

Let each of the readings be Y

Take average and find the mean X = (10.2+11+10.7+11+10.5)/5 = 53.4/5 = 10.68 m/s.

Take the difference between the data values and the mean and square them individually.

(10.2 - 10.68)² =(-0.48)² = 0.23

(11 - 10.68)² = 0.32² = 0.102

(10.7 - 10.68)² = (-0.02)² = 0.0004

(11-10.68)² =0.32² = 0.102

(10.5-10.68)² = (-0.18)² = 0.0324

Standard deviation =
`\sigma = \sqrt{(\sum(Y-X)^2 )/(n-1)}`

=
`√((0.23+0.102+0.0004+0.102+0.0324)/(5-1))`

=
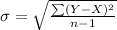
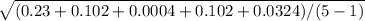
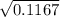`√(0.1167)` = 0.342 m/s

Error = Standard deviation /
`√(n)` = 0.342/5 = 0.153 .

Answer 2

mean = 10.68 m/s

standard deviation 0.3059

[/tex]\sigma_m = 0.14[/tex]

Step-by-step explanation:

1)
`Mean = ( 10.2+11+10.7+11+10.5)/(5)`

mean = 10.68 m/s

2 ) standard deviation is given as

`\sigma = \sqrt{ (1)/(N) \sum( x_i -\mu)^2}`

N = 5

`\sigma =\sqrt{ (1)/(5) \sum{( 10.2-10.68)^2+(11-10.68)^2 + (10.7- 10.68)^2+ (11- 10.68)^2++ (10.5- 10.68)^2`

SOLVING ABOVE RELATION TO GET STANDARD DEVIATION VALUE

\sigma = 0.3059

3) ERROR ON STANDARD DEVIATION

`\sigma_m = ( \sigma)/(√(N))`

`= (0.31)/(√(5))`

`\sigma_m = 0.14`