Answer:
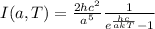
Step-by-step explanation:
The intensity of the radiation emitted by a black body with a certain temperature T and frequency
 , is given by Planck's law:
, is given by Planck's law:
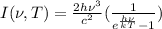
Considering the frequency range between
 and
and
 and
and
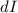 the amount of energy emitted in this frequency range. Since an increase in frequency means a decrease in wavelength. Then:
the amount of energy emitted in this frequency range. Since an increase in frequency means a decrease in wavelength. Then:

Now recall that
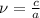 , differentiate both sides:
, differentiate both sides:

Replacing this in previous equation:
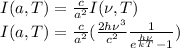
Rewriting
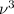 as
as
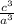 and
and
 as
as
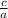
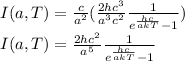
Finally, we obtain Planck's radiation law in terms of wavelength