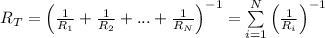Answer:
They're going to increase the total resistance as
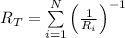
Step-by-step explanation:
If the resistors are in parallel, the potential difference is the same for each resistor. But the total current is the sum of the currents that pass through each of the resistors. Then
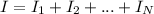
where
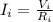
but
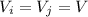 for
for
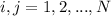
so
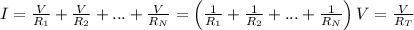
where