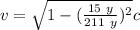Answer:
- The speed necessary is 0.99747 c
Step-by-step explanation:
We know that the equation for time dilation will be:
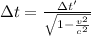
where Δt its the time difference measured from Earth, and Δt' is the time difference measured by the astronaut.
Lets work a little the equation
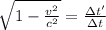
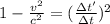
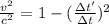
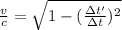
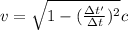
So, we got our equation. Knowing that Δt=211 years and Δt'=15 years
then