Answer:
(a): emf =
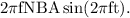
(b): Amplitude of alternating voltage = 20.942 Volts.
Step-by-step explanation:
Given:
- Area of the coil = A.
- Number of turns of coil = N.
- Magnetic field = B
- Rotation frequency = f.
(a):
The magnetic flux through the coil is given by
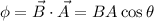
where,
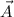 = area vector of the coil directed along the normal to the plane of the coil.
= area vector of the coil directed along the normal to the plane of the coil.
 = angle between
= angle between
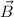 and
and
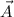 .
.
Assuming, the direction of magnetic field is along the normal to the plane of the coil initially.
At any time t, the angle which magnetic field makes with the normal to the plane of the coil is
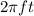
Therefore, the magnetic flux linked with the coil at any time t is given by
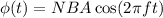
According to Faraday's law of electromagnetic induction, the emf induced in the coil is given by
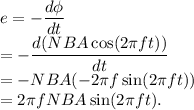
(b):
The amplitude of the alternating voltage is the maximum value of the emf and emf is maximum when

Therefore, the amplitude of the alternating voltage is given by
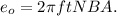
We have,
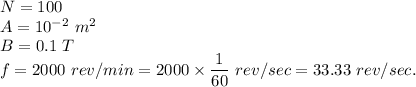
Putting all these values,
