Explanation:
We want to show that
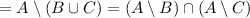
To prove it we just use the definition of

So, we start from the left hand side:
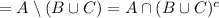 (by definition)
(by definition)
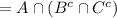 (by DeMorgan's laws)
(by DeMorgan's laws)
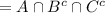 (since intersection is associative)
(since intersection is associative)
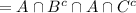 (since intersecting once or twice A doesn't make any difference)
(since intersecting once or twice A doesn't make any difference)
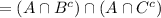 (since again intersection is associative)
(since again intersection is associative)
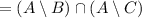 (by definition)
(by definition)
And so we have reached our right hand side.