Question

A jogger travels a route that has two parts. The first is a displacement of 3 km due south, and the second involves a displacement that points due east. The resultant displacement + has a magnitude of 3.85 km. (a) What is the magnitude of , and (b) what is the direction of + as a positive angle relative to due south? Suppose that - had a magnitude of 3.85 km. (c) What then would be the magnitude of , and (d) what is the direction of - relative to due south?

Answer 1

a) 2.41 km

b) 38.8°

Questions c and d are illegible.

Step-by-step explanation:

We can express the displacements as vectors with origin on the point he started (0, 0).

When he traveled south he moved to (-3, 0).

When he moved east he moved to (-3, x)

The magnitude of the total displacement is found with Pythagoras theorem:

d^2 = dx^2 + dy^2

Rearranging:

dy^2 = d^2 - dx^2

`dy = √(d^2 - dx^2)`

`dy = √(3.85^2 - 3^2)  = 2.41 km`

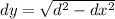
The angle of the displacement vector is:

cos(a) = dx/d

a = arccos(dx/d)

a = arccos(3/3.85) = 38.8°