Answer:
(a) A =
![[LT^(- 2)]](https://img.qammunity.org/2020/formulas/physics/college/w65ipj8oqpe1xzvoljbjl3lxf1ryd24iuw.png)
B =
![[LT^(- 3)]](https://img.qammunity.org/2020/formulas/physics/college/ml2jj08lpzppfqk031t5n369jnzz39ybjd.png)
![C = [LT^(- 5)]](https://img.qammunity.org/2020/formulas/physics/college/j85v1cbw6k6shifsu6itj4hfakjg5xcije.png)
(b) A =
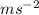
B =
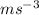
C =
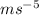
Solution:
The acceleration of a body is the rate at which the velocity of the body changes.
Thus
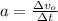
The SI unit of velocity of an object is
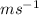 and its dimension is [LT^{- 1}] and for time, T the SI unit is second, s and dimension is [T] and hence
and its dimension is [LT^{- 1}] and for time, T the SI unit is second, s and dimension is [T] and hence
The SI unit and dimension for the acceleration of an object is
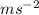 and [LT^{- 2}] respectively.
and [LT^{- 2}] respectively.
Now, as per the question:
acceleration, a =
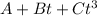
(a) Now, according to the homogeneity principle in dimension, the dimensions on both the sides of the eqn must be equal,
For the above eqn:
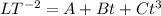
Thus the dimensions of :
A =
![[LT^(- 2)]](https://img.qammunity.org/2020/formulas/physics/college/w65ipj8oqpe1xzvoljbjl3lxf1ryd24iuw.png)
BT =
![[LT^(- 2)]](https://img.qammunity.org/2020/formulas/physics/college/w65ipj8oqpe1xzvoljbjl3lxf1ryd24iuw.png)
Thus for B
B =
![[LT^(- 3)]](https://img.qammunity.org/2020/formulas/physics/college/ml2jj08lpzppfqk031t5n369jnzz39ybjd.png)
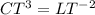
![C = [LT^(- 5)]](https://img.qammunity.org/2020/formulas/physics/college/j85v1cbw6k6shifsu6itj4hfakjg5xcije.png)
(b) For the units of A, B and C, we will make use of their respective dimensional formula from part (a)
where
L corresponds to length in meter(m)
T corresponds to time in seconds(s)
Now, for:
A =
![[LT^(- 2)] = ms^(- 2)](https://img.qammunity.org/2020/formulas/physics/college/q0nbyeycjq4i2235wdkbflj68c0pkira1a.png)
B =
![[LT^(- 3)] = ms^(- 3)](https://img.qammunity.org/2020/formulas/physics/college/dz3w8yajam7ngmgw4rxrnofza0co627w15.png)
C =
![[LT^(- 5)] = ms^(- 5)](https://img.qammunity.org/2020/formulas/physics/college/8nk9exdvv965se02kwc199dhygunt5lc6s.png)