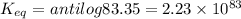Answer:
Equilibrium constant =
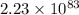
Step-by-step explanation:
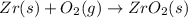
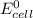 = 2.463 V
= 2.463 V
Equilibrium constant is related with
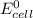 as
as

In standard condition,
T = 25 °C = 25 + 273 = 298 K
F = 96500 C mol^-1
R = 8.314
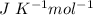
On substituting values, the above expression becomes:
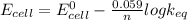
n = 2
At equilibrium,
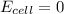
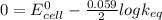
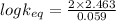
= 83.35