Question

Given vectors D (3.00 m, 315 degrees wrt x-axis) and E (4.50 m, 53.0 degrees wrt x-axis), find the resultant R= D + E. (a) Write R in vector form. (b) Write R showing the magnitude and direction in degrees.

Answer 1

• R = ( 4.831 m , 1.469 m )

• Magnitude of R = 5.049 m

• Direction of R relative to the x axis= 16°54'33'

Step-by-step explanation:

Knowing the magnitude and directions relative to the x axis, we can find the Cartesian representation of the vectors using the formula

`\vec{A}= | \vec{A} | \ ( \ cos(\theta) \ , \ sin (\theta) \ )`

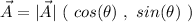
where
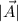`| \vec{A} |` its the magnitude and θ.

So, for our vectors, we will have:

`\vec{D}= 3.00 m \ ( \ cos(315) \ , \ sin (315) \ )`

`\vec{D}=  ( 2.121 m , -2.121 m )`

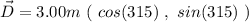
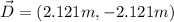
and

`\vec{E}= 4.50 m \ ( \ cos(53.0) \ , \ sin (53.0) \ )`

`\vec{E}= ( 2.71 m , 3.59 m )`

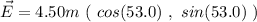
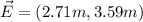
Now, we can take the sum of the vectors

`\vec{R} = \vec{D} + \vec{E}`

`\vec{R} = ( 2.121 \ m , -2.121 \ m ) + ( 2.71 \ m , 3.59 \ m )`

`\vec{R} = ( 2.121 \ m  + 2.71 \ m , -2.121 \ m + 3.59 \ m )`

`\vec{R} = ( 4.831 \ m , 1.469 \ m )`

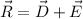
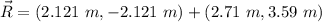
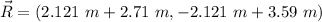
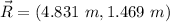
This is R in Cartesian representation, now, to find the magnitude we can use the Pythagorean theorem

`|\vec{R}| = √(R_x^2 + R_y^2)`

`|\vec{R}| = √((4.831 m)^2 + (1.469 m)^2)`

`|\vec{R}| = √(23.338 m^2 + 2.158 m^2)`

`|\vec{R}| = √(25.496 m^2)`

`|\vec{R}| = 5.049 m`

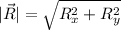
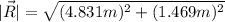
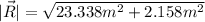
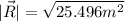
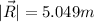
To find the direction, we can use

`\theta = arctan((R_y)/(R_x))`

`\theta = arctan((1.469 \ m)/(4.831 \ m))`

`\theta = arctan(0.304)`

`\theta = 16\°54'33''`

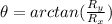
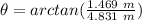
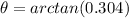
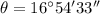
As we are in the first quadrant, this is relative to the x axis.