Answer:
- R = ( 4.831 m , 1.469 m )
- Direction of R relative to the x axis= 16°54'33'
Step-by-step explanation:
Knowing the magnitude and directions relative to the x axis, we can find the Cartesian representation of the vectors using the formula
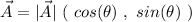
where
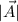 its the magnitude and θ.
its the magnitude and θ.
So, for our vectors, we will have:
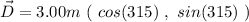
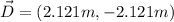
and
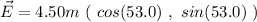
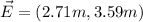
Now, we can take the sum of the vectors
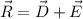
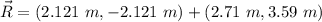
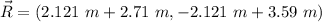
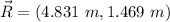
This is R in Cartesian representation, now, to find the magnitude we can use the Pythagorean theorem
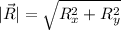
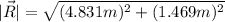
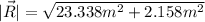
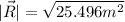
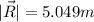
To find the direction, we can use
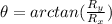
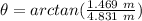
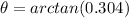
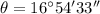
As we are in the first quadrant, this is relative to the x axis.