Question

Show that Z2[i] = a,b € Z2 is not a field

Answer 1

Explanation:

On a field every element different from 0 should have a multiplicative inverse. Let's check that in Z2[i] not ALL nonzero elements have multiplicative inverses.

Z2 is made of two elements: 0 and 1, and so Z2[i] is made of four elements: 0+0i,0+1i, 1+0i, 1+1i (which we can simplify from now on as 0, i, 1, 1+i respectively). Now, let's check that the element 1+i doesn't have a multiplicative inverse (we can do this by showing that no matter what we multiply it by, we're not getting 1, which is the multiplicative identity)

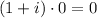`(1+i)\cdot 0 = 0` (which is NOT 1)

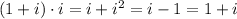`(1+i)\cdot i = i+i^2=i-1=1+i` (which is NOT 1) (remember -1 and 1 are the same in Z2)

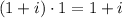`(1+i)\cdot 1 = 1+i` (which is NOT 1)

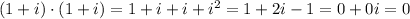`(1+i)\cdot (1+i) = 1+i+i+i^2=1+2i-1=0+0i=0` (which is NOT 1) (remember 2 is the same as 0 in Z2)

Therefore the element 1+i doesn't have a multiplicative inverse, and so Z2[i] cannot be a field.