Question

An air bubble at the bottom of a lake 36.0 m deep has a volume of 1.22 cm^3. If the temperature at the bottom is 5.9°C and at the top 16.0°C, what is the volume of the bubble just before it reaches the surface?

Answer 1

volume of the bubble just before it reaches the surface is 5.71 cm³

Step-by-step explanation:

given data

depth h = 36 m

volume v2 = 1.22 cm³ = 1.22 ×
`10^(-6)` m³

temperature bottom t2 = 5.9°C = 278.9 K

temperature top t1 = 16.0°C = 289 K

to find out

what is the volume of the bubble just before it reaches the surface

solution

we know at top atmospheric pressure is about P1 =
`10^(5)` Pa

so pressure at bottom P2 = pressure at top + ρ×g×h

here ρ is density and h is height and g is 9.8 m/s²

so

pressure at bottom P2 =
`10^(5)` + 1000 × 9.8 ×36

pressure at bottom P2 =4.52 ×
`10^(5)` Pa

so from gas law

`(P1*V1)/(t1) = (P2*V2)/(t2)`

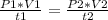
here p is pressure and v is volume and t is temperature

so put here value and find v1

`(10^(5)*V1)/(289) = (4.52*10^(5)*1.22)/(278.9)`

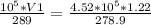
V1 = 5.71 cm³

volume of the bubble just before it reaches the surface is 5.71 cm³